엑셀 (Excel)을 이용해서 Q-Q plot 만들고 정규성 검증하기
분석 결과의 정규성 검증은 다음과 같은 상황에서 확인이 필요하다.
단일 그룹의 자료에서 이상치 (outlier) 확인 방법으로 사용된다.
예를 들어, 분석 방법의 비교 테스트에서 동일 시료를 각기 다른 방법으로 실험해서 결과의 편차를 확인한다.
단일 분석법의 결과에서 이상치 (outlier)가 존재한다면
분석법의 편차는 증가해서 방법 간의 차이가 있다고 평가될 수 있다.
데이터의 비교 분석 및 통계 처리 전에 정규성 확인되는 것이
데이터 처리 결과의 신뢰도를 얻을 수 있기 때문이다.
Q-Q plot (Quantile-Quantile plot)은 데이터를 일정 간격으로 나열하고
정규분포의 순위 (Quantile)에 범위에 분포하는지 확인하는 그래프이다.
두 분석법의 비교 테스트의 시료 개수는 대략 30 개를 권장하고 있어서
각 분석법의 30개의 결과를 정규성 검증을 시행하는 내용을 엑셀로 설명하려고 한다.
직접 제작한 엑셀 파일로 설명하고, 파일을 공유하려고 한다.
해당 내용은 아래 홈페이지를 참고해서 작성하였다.
Desc – QQ and Dot Plots | Real Statistics Using Excel
On this webpage, we describe in detail the QQ Plot and Dot Plot options of the Real Statistics Descriptive Statistics and Normality data analysis tool. We use the example data shown in Figure 3 of the Descriptive Statistics and Normality Tool, repeated in
real-statistics.com
1. 측정된 결과는 엑셀 파일 "Law Data"라고 표기된 표의 Results 아래에 입력한다.
2. 입력된 결과는 바로 옆에 "Normality test: Q-Q plot and Shapiro-Wilk"라고 표기된 아래에 내용이 나타난다.
| Interval | Results | Normal Quantiles |
| 1 | 1.000 | -2.128 |
| 3 | 2.500 | -1.645 |
| 5 | 3.500 | -1.383 |
| 7 | 3.900 | -1.192 |
| 9 | 4.500 | -1.036 |
| 11 | 4.500 | -0.903 |
| 13 | 5.000 | -0.784 |
| 15 | 5.100 | -0.674 |
Interval: 일정간격의 누적값으로 정규분포의 순위를 계산하기 위한 임의로 설정된 값이다.
Results: 측정된 입력한 값을 낮은 값부터 순서대로 나열된 결과이다.
이때 엑셀 함수 "=QSORT(B4:B33)"를 사용해면 해당 범위의 데이터를 오름차순으로 정렬해 준다.
Normal Quantiles: Interval 값의 정균분포 순위를 환산한 값이다.
이때 엑셀 함수
"=NORM.S.INV(probability)"를 사용했다.
probability 값은
Interval 값/ (Interval 개수✕2)으로 계산되었다.
해당 함수는 표준 정규 누적 분포의
역함수를 계산하고,
그 정규 분포는 평균이 0 과 표준편차가 1인
정규 분포를 사용한다고 했다.
probability 값이 0과 1이 되면 계산 오류가
발생하기 때문에 interval 간격을 2로 설정하고
(홀수값), probability 값을 전체 개수의 2배로
계산하면 (= 59 / 60) 최대값이 1 보다 작은 값으로 계산되어 오류를 방지할 수 있다.
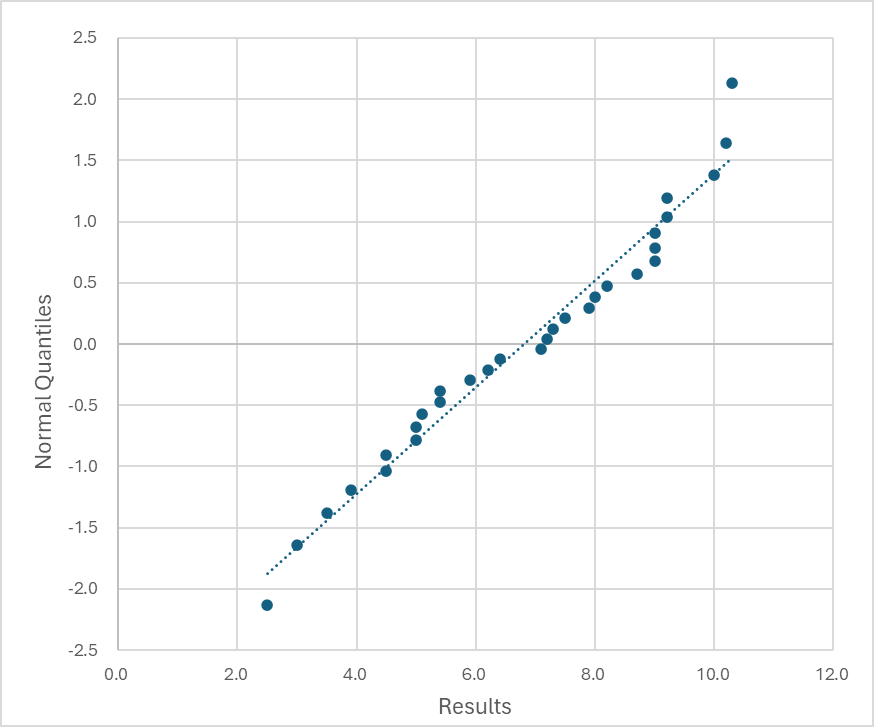
Q-Q plot은 Resuts와 Normal Quantiles을 이용해서 산점도 그래프로 작성했다.

대략적인 분포의 패턴을 확인하기 위해서
직선의 추세선을 추가해서 점선으로 표기했다.
정규분포를 나타내는 데이터라면,
추세선에 주변에 배치되어야 한다.
하지만, 높은 값의 일부 결과들이
다른 데이터들과 달리 추세선에서 많이 벗어나 있다.
그래프는 전반적인 데이터 패턴을 볼 수 있기에
오류 데이터를 쉽게 확인이 가능하다.
단점은 주관적인 평가가 이루어지기 때문에
추가적인 객관적 평가 내용이 필요하다.
모집단 (전체 집단)이 아닌 표본에서
정규성 검증에 사용하는 통계방법은
"Shapiro-Wilk test"를 사용한다.
| Shapiro-Wilk Test | |
| n = | 30 |
| W statistic = | 0.8875 |
| p-value = | 0.0042 |
| alpha = | 0.05 |
| Normality = | No |
참고 자료로 이용했던 Real Statistics
홈페이지를 방문하면,
엑셀 관련 추가기능을 다운 받아서 엑셀 추가 기능을 설치할 수 있다.
https://real-statistics.com/free-download/
엑셀 추가 기능 파일 "XRealStats.xlam"을 받아서 추가 기능 설정 창에서 추가할 수 있다.
추가 기능이 설치되면 다음과 같은 함수들을 엑셀에서 사용할 수 있다.
(위에서 사용한 QSORT 함수도 해당 기능이 추가되어야 사용이 가능하다.)
검정통계량 (W statistic)은 엑셀 함수 "=SHAPIRO(Results)"를 사용한다.
검증은 p-value로 평가되는데 엑셀 함수 "=SWTEST(Results)"를 사용한다.
95% 신뢰 구간을 기반으로 p-value 값이 0.05 (alpha) 값보다 낮으면
모든 데이터들이 정규분포 범위에 포함되지 않다고 평가된다. 일부 데이터들이 정규분포를 벗어난 범위 존재하는 것이다.
일반적으로는 벗어난 데이터들은
제거하는 방식을 선택하지만
내용을 비교하기 위해서 벗어난 데이터의 값을
수정해서 내용을 확인했다.
일부 증가된 값들을 낮은 값으로 변경해서 Q-Q plot을 다시 작성하면 다음과 같은 그래프로 나타났다.
추세선에 데이터들이 인접한 것을 확인할 수 있었고,
Shapiro-Wilk test 결과에서 정규성이 있는 것으로 검증되었다.
| Shapiro-Wilk Test | |
| n = | 30 |
| W statistic = | 0.9587 |
| p-value = | 0.2860 |
| alpha = | 0.05 |
| Normality = | Yes |
해당 자료는 엑셀 파일로 공유합니다.
"XRealStats.xlam" 의 추가 기능 설치없이
계산이 필요하다면,
QQ plot_V2 버전 파일은
엑셀 기존 함수만 사용해서 제작했다.
이 버전의 경우 Shapiro-Wilk test의
p-value 확인이 불가하고,
검정 통계량 (W)을 확인 후
정규성 검증에 필요한 검정 통계량의 분위수 값과
비교해야 하는 번거러움이 있다.
계산값이 기존 함수와 차이는 있지만,
정규성 검증에는 문제가 없었다.
추가 의견 또는 오류에 대한 의견이 있으시면
댓글 부탁드립니다.
감사합니다.
'데이터 처리 방법' 카테고리의 다른 글
| [Excel+Python] 정규성 검증: Shapiro-Wilk test (0) | 2024.02.19 |
|---|---|
| [Excel] 분석법 비교 방법 : Bland-Altman Plot (반복 측정 결과) (1) | 2024.02.06 |
| [Excel] 분석법 비교 방법 : Bland-Altman Plot (단일 측정 결과) (0) | 2024.02.05 |
| [Excel] 재현성 (Precision) 평가 방법 : 분산 분석 (ANOVA) (2) | 2024.01.15 |
| [Excel] 측정 방법의 비교 분석 : Deming Regression (0) | 2023.11.19 |