재현성 (Precision) 평가에 사용되는 분산 분석 (ANOVA)을 엑셀로 알아보자!
분석결과의 검증 (validation) 내용 중 하나인 재현성 (Precision) 평가는
단일 측정 농도의 반복 측정 결과를 통해서 확인된다.
기본적인 평가 방법은 반복 측정의 결과의 상대표준편차 (RSD: relative standard deviation)을 확인하고,
해당 분석법의 RSD 허용기준 이하의 값을 가지는지 확인하면 된다.
재현성 평가 방법은 단일 측정 결과 이외에 다양한 농도와 다른 분석일까지 고려해서 평가되므로
다양한 요소를 평가할 수 있는 자료 정리 방법이 중요하게 된다.
예를 들어, 3가지 농도의 3회 반복 측정을 3일 동안 진행해서 재현성을 평가한다면
각 농도별 9개의 결과와 전체 27개의 데이터가 얻어진다.
반복측정 결과에서 확인하는 내용은
2가지 변수 (농도, 날짜)가 재현성에 영향을 미치는지 확인하는 것이다.
결과 정리는 하루 동안의 재현성을 확인하는 반복성 (repeatability) 값은
각 농도별 반복측정 결과로 다음과 같이 계산한다.
분석법 허용기준이 %RSD로 제시되기 때문에
실험에서 확인된 %RSD 값이 허용기준보다 낮으면 재현성은 문제가 없다고 보고된다.
반복성은 %RSD 로 평가되지만, 같은 실험을 3일 동안 결과는
어떻게 평가되어야 하는지 의문이 생길 수 있다.
분석법 가이드라인의 재현성 내용에 아래와 같은 내용이 기술되어 있다.
Between-run (intermediate) precision and accuracy should be calculated by combining the data from all runs.
참고문헌: Guideline, I. H. (2022). Bioanalytical method validation and study sample analysis M10. ICH Harmonised Guideline: Geneva, Switzerland.
위 예시의 실험 내용에서 Between-run 은 다른 날에 테스트를 나타내는 것으로 해석이 가능하며,
이 때 재현성은 모든 실험의 데이터로 계산하라고 기술되어 있다.
즉, 동일 농도의 3일 결과 총 9개의 결과를 이용해서 %RSD 값을 계산하고,
허용기준 %RSD 보다 낮은지 확인하면 된다.
하지만, 상황에 따라서는 정밀성 추가 검증 또는 자세한 자료 검토에
ANOVA 테스트가 사용될 수 있다.
ANOVA 테스트는 다양한 종류가 있기 때문에 적절히 잘 사용하는 것이 필요하다.
정밀성 분석에는 일원배치 분산분석 (One-way ANOVA)와 이원배치 분산분석 (Two-way ANOVA)이 사용될 수 있다.
아래 적용된 예시를 보면 분산분석이 사용된 것을 볼 수 있다.
Precision was expressed in terms of intra- and interday CV (%), calculated by single-nested ANOVA of daily means. The accuracy was expressed in terms of mean recoveries (%).
참고문헌: Farré-Segura, J., Le Goff, C., Lukas, P., Cobraiville, G., Fillet, M., Servais, A. C., ... & Cavalier, E. (2022). Validation of an LC-MS/MS Method Using Solid-Phase Extraction for the Quantification of 1-84 Parathyroid Hormone: Toward a Candidate Reference Measurement Procedure. Clinical Chemistry, 68(11), 1399-1409.
분산분석 중에서도 single-nested ANOVA"는 일원배치 분산분석을 지칭하며,
분석 결과 값이 여러 변수에 중첩되어 있지만, 날짜 변수에 따른 분산분석을 수행했다는 것이다.
그 이외에 재현성 평가를 위해서 "반복있는 이원배치 분산분석 (Two-factor with replication ANOVA)" 도 사용된다.
엑셀에는 이원배치 분산분석이 "반복없는" 또는 " 반복있는" 두 가지 경우로 나눠져 있다.
변수 2가지 고려해서 분산 분석하는 방법이 반복없는 이원배치 분산분석이고,
변수 2개에 반복 측정이 포함되는 경우라면 "반복있는 이원배치 분산분석" 이 사용된다.
이원배치 분산분석의 유용성을 설명하려면,
일원배치 분산분석의 결과를 먼저 확인해 봐야 한다.
2 개 이상의 각 그룹의 데이터 분산 차이를 확인하는 방법이 분산분석으로
이때 변수 1개에 대한 분산 차이를 검증하는 것이 일원배치 분산분석이다.
예를 들어, 실험 결과에서 분석일에 대한 결과 차이가 있는지 확인하고 싶다면
다음과 같이 자료를 정리해서 엑셀로 통계분석을 실시한다.
| Low level | Repeat 1 | Repeat 2 | Repeat 3 | Repeat 4 | Repeat 5 |
| Day1 | 1.24 | 1.03 | 1.27 | 1.27 | 1.19 |
| Day2 | 1.31 | 1.01 | 1.16 | 1.21 | 1.07 |
| Day3 | 1.07 | 1.02 | 1.02 | 1.03 | 1.18 |
| Day4 | 1.32 | 1.14 | 1.16 | 1.12 | 1.31 |
| Day5 | 1.11 | 1.30 | 1.25 | 1.07 | 1.19 |
위 실험 내용은 Low level의 농도를 1회 분석마다 5회 반복측정하고, 5일 동안 실험한 결과이다.
엑셀 메뉴에 "데이터 > 데이터 분석" 을 선택하면, 다음과 같은 통계 데이터 분석 창이 나타난다.

"분산분석: 일원 배치법"을 선택하면 다음과 같이 데이터의 영역을 설정하고
반복측정 결과 값이 열로 배치되어 있기 때문에 데이터 방향을 열로 선택하고 결과를 확인한다.

| 분산 분석: 일원 배치법 | ||||||
| 분산 분석 | ||||||
| 변동의 요인 | 제곱합 | 자유도 | 제곱 평균 | F 비 | P-값 | F 기각치 |
| 처리 | 0.069425 | 4 | 0.017356 | 1.871796 | 0.154879 | 2.866081 |
| 잔차 | 0.18545 | 20 | 0.009273 | |||
| 계 | 0.254875 | 24 | ||||
결과 내용을 살펴보면, "인자의 수준"은 분산을 확인하고자 하는 변수에 해당되며
해당 변수 여기서는 날짜에 대한 분산 차이는 분산 분석 결과에 결과에 나타난다.
"F 비" 값이 "F 기각치" 보다 낮은 값으로 확인되었기 때문에
날짜 마다 측정된 결과의 분산은 차이가 같을 확률이 높다고 설명된다.
"P-값"이 확률을 나타내는 내용으로 동일한 분산이 나타날 확률 95% 신뢰구간을 벗어나면
0.05 보다 낮은 값으로 계산되어 분산 차이가 있는 날짜의 결과가 있다고 해석된다.
현재 결과에서 "P-값"이 0.15 > 0.05 보다 높은 값을 가지므로
날짜 마다 측정된 결과에는 분산 차이가 없으므로
해당 분석 방법은 다른 날짜에도 재현성 있는 결과를 보여준다고 설명할 수 있다.
일원배치 분산분석의 단점은 변수가 1에 대한 평가만 가능하므로
위와 같은 실험의 경우 농도의 변수 (농도 레벨: low, medium, high)가 있기 때문에
일원배치 분산분석을 농도 마다 확인해야 하는 번거로운 작업이 수반된다.
그래서 두 변수 (날짜, 농도)의 차이에도 분산 차이가 발생하는지 확인하는 방법이
이원배치 분산분석이고, 재현성 테스트는 반복 측정을 기반으로 하기 때문에
"반복있는 이원배치 분산분석"이 필요한 것이다.
"반복있는 이원배치 분산분석 (Two-factor with replication ANOVA)"을 수행하기 위해서는
다음과 같은 형식으로 데이터를 정리해야 한다.
| Day1 | Day2 | Day3 | Day4 | Day5 | |
| Low | 1.24 | 1.31 | 1.07 | 1.32 | 1.11 |
| Low | 1.03 | 1.01 | 1.02 | 1.14 | 1.30 |
| Low | 1.27 | 1.16 | 1.02 | 1.16 | 1.25 |
| Low | 1.27 | 1.21 | 1.03 | 1.12 | 1.07 |
| Low | 1.19 | 1.07 | 1.18 | 1.31 | 1.19 |
| Medium | 5.43 | 5.74 | 5.31 | 5.20 | 6.09 |
| Medium | 5.65 | 5.74 | 5.44 | 5.73 | 6.25 |
| Medium | 6.14 | 6.14 | 5.48 | 6.14 | 6.01 |
| Medium | 6.18 | 5.01 | 5.15 | 5.79 | 5.14 |
| Medium | 6.29 | 5.24 | 5.85 | 6.08 | 5.23 |
| High | 11.30 | 10.78 | 11.03 | 11.43 | 10.87 |
| High | 11.07 | 10.86 | 10.43 | 10.20 | 11.48 |
| High | 10.36 | 10.16 | 11.48 | 11.08 | 10.32 |
| High | 10.59 | 10.46 | 10.58 | 11.18 | 10.20 |
| High | 11.04 | 10.29 | 10.84 | 11.16 | 10.62 |
반복측정의 결과들이 세로로 나열되도록 배치되어야 한다.
엑셀로 통계분석을 진행해야 하기 때문에 이런 배치가 필요하다.
엑셀 메뉴에 "데이터 > 데이터 분석" 을 선택해서,
통계 데이터 분석 창에 나타난 목록에서 "분산분석: 반복 있는 이원 배치법"을 선택한다.
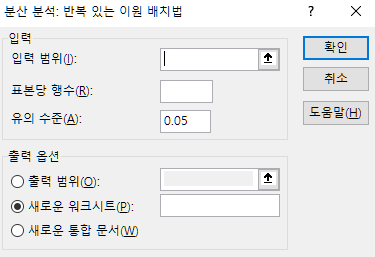
입력 범위는 항목명까지 포함해서 선택하고,
"표본당 행수"에 반복 측정의 수를 입력한다.
여기에는 데이터 방향의 선택이 없기 때문에
반복 측정의 데이터가 세로 방향으로 나열되어야 한다.
엑셀로 실행하는 방식은 일원배치 분산분석과 동일하다.

| 분산 분석: 반복 있는 이원 배치법 | ||||||
| 분산 분석 | ||||||
| 변동의 요인 | 제곱합 | 자유도 | 제곱 평균 | F 비 | P-값 | F 기각치 |
| 인자 A (행: 농도) | 1160.602 | 2 | 580.3008 | 4964.834 | 2.28E-67 | 3.150411 |
| 인자 B (열: 날짜) | 0.832249 | 4 | 0.208062 | 1.780102 | 0.144657 | 2.525215 |
| 교호작용 | 0.710085 | 8 | 0.088761 | 0.759402 | 0.639375 | 2.096968 |
| 잔차 | 7.012934 | 60 | 0.116882 | |||
| 계 | 1169.157 | 74 | ||||
이원배치 분산분석 해석은 이전 일원배치 분산분석과 동일하지만,
변수가 2개 이므로 변수별 결과가 각각 나타나게 된다.
농도 변수의 결과는 "인자 A (행)"에서 확인되며,
"P-값" 이 0.05보다 낮은 값으로 계산되어 농도 레벨에 따른 분산차이는 있는것으로 해석된다.
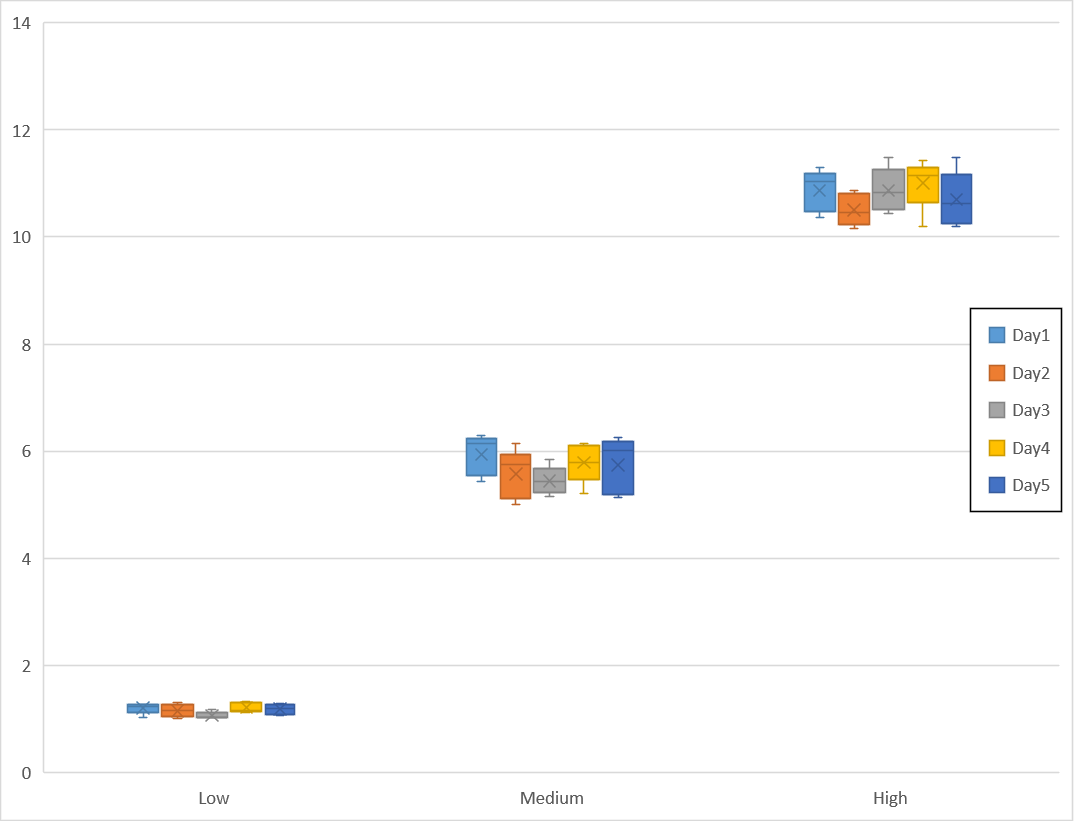
그래프 내용을 확인해도 농도 차이로 분산이 확연히 차이나는 것이 확인된다.
농도가 증가하면 장비 측정값도 비례하고 이와 같이 측정 오차도 같이 증가하는 것은 일반적인 현상이다.
그래서 농도 증가로 분산 차이가 발생하는 것은 재현성 평가 내용에 포함되지 않는다.
실험 날짜가 다른 경우 분산 차이가 발생하는 확인된 내용은
"인자 B (열)"의 "P-값" 으로 확인되며,
"P-값" 은 0.05보다 높은 값으로 계산되어 날짜에 따른 분산 차이가 없는 것으로 해석된다.
각 농도의 분산이 실험 날짜에 대해서 차이는 없다는 통계적으로 검증되면,
해당 분석법은 다른 날짜와 농도 차이에도 재현성이 있다고 설명된다.
다른 실험 결과의 데이터를 이용해서 위와 같이 그래프를 작성했다.
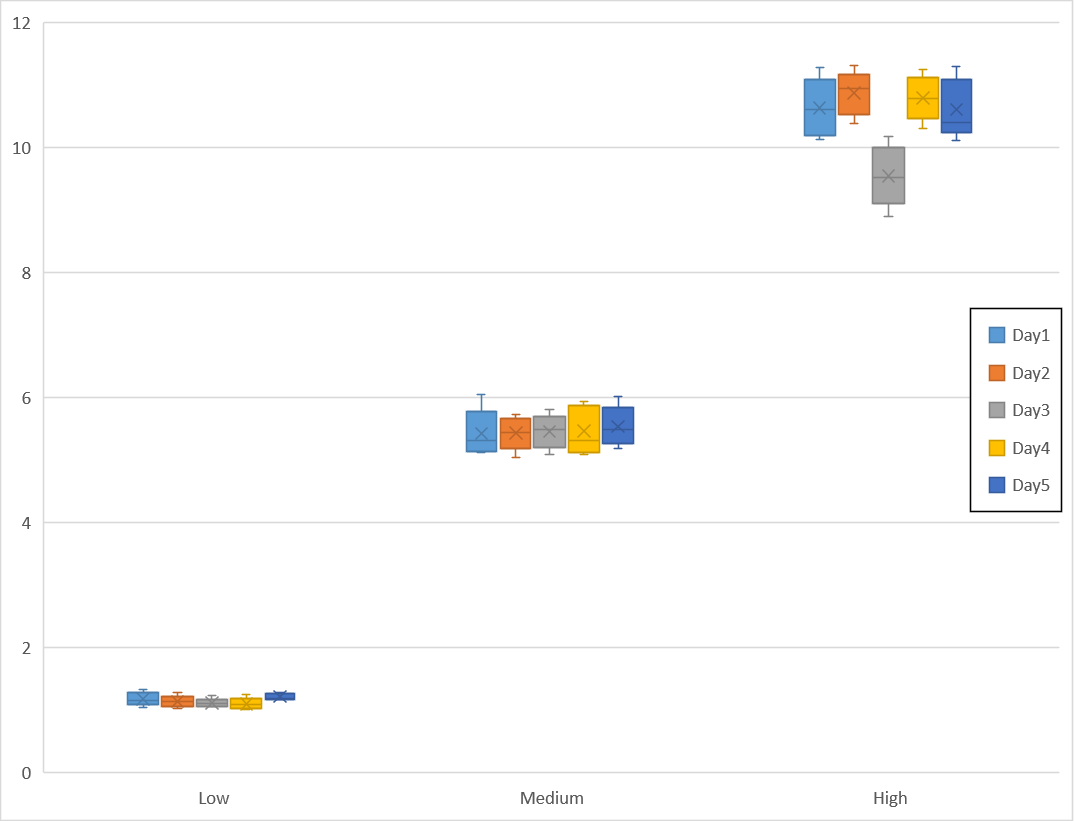
High level의 3일 분석 결과를 보면 다른 결과 분포에서 벗어난 것이 확인된다.
전체 실험 결과와 개별 날짜에 분석한 결과에서는 분석법의 허용기준 %RSD 15%를 초과한 내용은 확인되지 않았다.
추가 검증을 위해서 이원배치 분산분석을 시행한 결과는 다음과 같다.
| 분산 분석: 반복 있는 이원 배치법 | ||||||
| 분산 분석 | ||||||
| 변동의 요인 | 제곱합 | 자유도 | 제곱 평균 | F 비 | P-값 | F 기각치 |
| 인자 A (행: 농도) | 1093.987 | 2 | 546.9936 | 5415.26 | 1.71E-68 | 3.150411 |
| 인자 B (열: 날짜) | 2.083159 | 4 | 0.52079 | 5.155841 | 0.001227 | 2.525215 |
| 교호작용 | 3.826955 | 8 | 0.478369 | 4.735877 | 0.000155 | 2.096968 |
| 잔차 | 6.06058 | 60 | 0.10101 | |||
| 계 | 1105.958 | 74 | ||||
결과에서 "인자 A"의 결과는 이전처럼 농도에 따른 분산 차이가 나는 것이 확인되었지만,
측정 결과의 일반적인 현상으로 해석된다.
분석 날짜의 분산 차이를 확인한 "인자 B"의 결과에서
"P-값" 은 0.05 보다 낮은 0.001227로 통계적으로 유의한 분산 차이가 발생했다는 것이 확인되었다.
이처럼 모든 농도의 날짜별 그룹 15 중 하나의 그룹에서 분산 차이가 발생하면
"P-값" 이 통계적으로 유의한 차이를 보여주게 된다.
교호작용 (Interaction Effect) 내용은 두 변수의 상호작용으로 분산 차이가 발생하는 것을 확인한 것이다.
처음 이원배치 분산분석 결과에서는 "P-값" 이 0.64로 0.05 보다 큰 값을 보이고 있어서
농도와 날짜 변수의 상호작용이 없는 것이 확인되었다.
하지만, 두번째 이원배치 분산분석 결과에서는 "P-값" 이 0.000155로 0.05 보다 낮은 값을 보이고 있어서
농도가 증가하면서 날짜 변수에 따른 분산이 증가한다는 상호작용이 나타나고 있다는 것이 확인된 것이다.
해당 결과는 재현성 내용과 관련이 없는 부분으로
재현성 오차 원인을 찾기 위한 추가 정보라고 생각해야 한다.
두 번째 실험 결과에서 가장 높은 농도의 3일 결과에서
정확성 오차가 크게 발생된 것이 확인되었고,
이 부분은 무작위 오차로 발생된 것인지 아니면 다른 원인으로 발생한 문제인지 추가 검토가 필요하다.
하지만, 다른 날짜에는 추가 오차가 나타나지 않는 것으로 보여서
무작위 오차로 발생한 일시적 오류로 추정되므로 추후 상황을 지켜볼 필요가 있다.
이원배치 분산분석은 단일 테스트를 통해서 통계적 결과를 얻을 수 있다는 장점이 있다.
하지만, 두 번째 실험 결과처럼 문제점이 확인되면
사후 분석으로 개별 일원배치 분산분석을 시행해야
어떤 그룹의 데이터가 문제가 발생했는지 확인이 가능하다.
이처럼 ANOVA 테스트는 분산 차이를 확인하기 위한 도구로 사용되며,
재현성의 자세한 내용 검토 및 검증을 위해서 사용될 수 있다.
하자만, 적합한 ANOVA 테스트를 사용하는 것이 필요하므로 주의가 필요하다.
자세한 내용은 첨부된 엑셀 파일을 참고하면 설명된 모든 내용을 확인할 수 있다.
'데이터 처리 방법' 카테고리의 다른 글
| [Excel+Python] 정규성 검증: Shapiro-Wilk test (0) | 2024.02.19 |
|---|---|
| [Excel] 분석법 비교 방법 : Bland-Altman Plot (반복 측정 결과) (1) | 2024.02.06 |
| [Excel] 분석법 비교 방법 : Bland-Altman Plot (단일 측정 결과) (0) | 2024.02.05 |
| [Excel] 측정 방법의 비교 분석 : Deming Regression (0) | 2023.11.19 |
| [Excel] 정규성 검증 : Q-Q plot 만들기 (0) | 2023.11.06 |