비선형 검정곡선 4-parameter equation을 엑셀 "파이썬"으로 만들기
이전 글에서 엑셀의 해 찾기 기능으로 비선형 검정곡선 4-parameter equation을 만들어 보았다.
2025.03.30 - [기기분석 데이터] - [Excel] 비선형 검정곡선 만들기 : 4-Parameter Equation
[Excel] 비선형 검정곡선 만들기 : 4-Parameter Equation
비선형 검정곡선 4-parameter equation을 엑셀 "해 찾기"로 만들기엑셀은 기본적으로 선형 회귀분석 (Regression) 기능을 제공하고 있어서 직선의 검정곡선을 만들기에는 어려움이 없다. 2023.11.24 - [분류
analchem.tistory.com
하지만, 아쉬운 부분이 있었다.
초기 설정값이 최적값보다 큰 차이를 가지는 경우에는
여러차례 해 찾기 기능을 적용해야 최적값을 찾을 수 있었고,
자동 계산되지 않고 해 찾기 기능을 실행해야 결과를 확인할 수 있었다.
앞서 언급한 불편함이 개선되어 전체적인 계산이 자동으로 작성된다면,
동일한 구성의 실험 데이터를 계산된 서식에 붙여넣고 바로 결과를 확인할 수 있어서 편리하다.
최근 MS 365 엑셀은 파이썬 기능을 제공하며,
파이썬은 다양한 통계적 방법들을 지원하고 있기 때문에
4-parameter equation을 찾는데 활용할 수 있을 것으로 생각했다.
AI (인공지능)에게 물어보니 가능한 코딩 내용까지 확인해 주었다.
막상 코딩 작성 내용을 엑셀 파이썬에 입력했을 때는 원하는 결과가 나타나지 않아서
여러차례 시행착오 과정을 거쳐 자동 계산의 결과를 얻을 있었다.
그 내용을 정리해서 자세히 설명하려고 한다.
우선 엑셀 메뉴에 "수식 > Python 삽입" 이 나타나지 않으면
이 방법이 불가하기 때문에 MS 365 버전의 엑셀이 꼭 필요하다.
엑셀 파이썬 버전에서 실행가능한 코딩은 아래와 같다.
# 분석 방법 라이브러리 불러오기
from scipy.optimize import curve_fit
# 4PL (4-parameter logistic) 모델 함수 정의
def logistic4(x, A, D, B, C): return D + (A - D) / (1 + (x / C) ** B)
# Excel 데이터 가져오기
data = xl("A1:B7", headers = True) # A1:B7 데이타 범위
data.columns = ["X", "Y"]
x_data = data["X"].dropna().to_numpy() # Excel 열 'X' 데이터
y_data = data["Y"].dropna().to_numpy() # Excel 열 'Y' 데이터
# 초기값 가져오기
A0 = xl("J13")
D0 = xl("J14")
B0 = xl("J15")
C0 = xl("J16")
# 초기값 설정
initial_guesses = [A0, D0, B0, C0]
# 4PL 회귀 분석
params1, covariance = curve_fit(logistic4, x_data, y_data, p0=initial_guesses)
# 결과 반환 (A, D, B, C)
params1
기본적인 계산에 필요한 라이브러리 numpy와 데이터를 형식 설정을 위한 라이브러리 pandas가 필요하지만
엑셀에는 기본적으로 파이썬을 수행할때 불러오기를 실행하며, 그 중에 numpy, pandas가 포함되어 있다.
아래 내용은 엑셀 파이썬에서 기본적으로 불러오는 라이브러리 목록이다.
# The following import statements are pre-loaded.
import numpy as np import pandas as pd
import matplotlib.pyplot as plt
import statsmodels as sm
import seaborn as sns
import excel
import warnings
warnings.simplefilter('ignore')
# Set default conversions for the xl() function.
excel.set_xl_scalar_conversion(excel.convert_to_scalar) excel.set_xl_array_conversion(excel.convert_to_dataframe)
추가로 필요한 라이브러리는 불러오기 작업이 필요하다.
수식에 적합한 상수를 찾아주는 라이브러리는 "scipy> optimize > curve_fit" 을 사용했다.
scipy의 curve_fit 함수는 잔차를 최소화해서 수식의 상수값을 찾아주는 방법으로
비선형 곡선의 상수값을 찾아주는 Levenberg-Marquardt algorithm이 기본 설정으로 되어있다.
참고: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html
curve_fit — SciPy v1.15.2 Manual
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.optimize import curve_fit >>> def func(x, a, b, c): ... return a * np.exp(-b * x) + c Define the data to be fit with some noise: >>> xdata = np.linspace(0, 4, 50) >>> y = func(xdata,
docs.scipy.org
curve_fit 함수는 수식에 정의가 필요해서 4-parameter equation 설정과
초기값이 필요하기 때문에 임의의 값을 가져오는 내용의 설정이 필요하다.
모든 설정이 끝나면 실험 테이터와 초기값을 함수 양식에 맞게 대입하면 최적화된 상수값을 바로 확인할 수 있다.
아래 화면은 파이썬 코딩을 엑셀에 입력하고 실행하는 과정을 보여주는 내용이다.
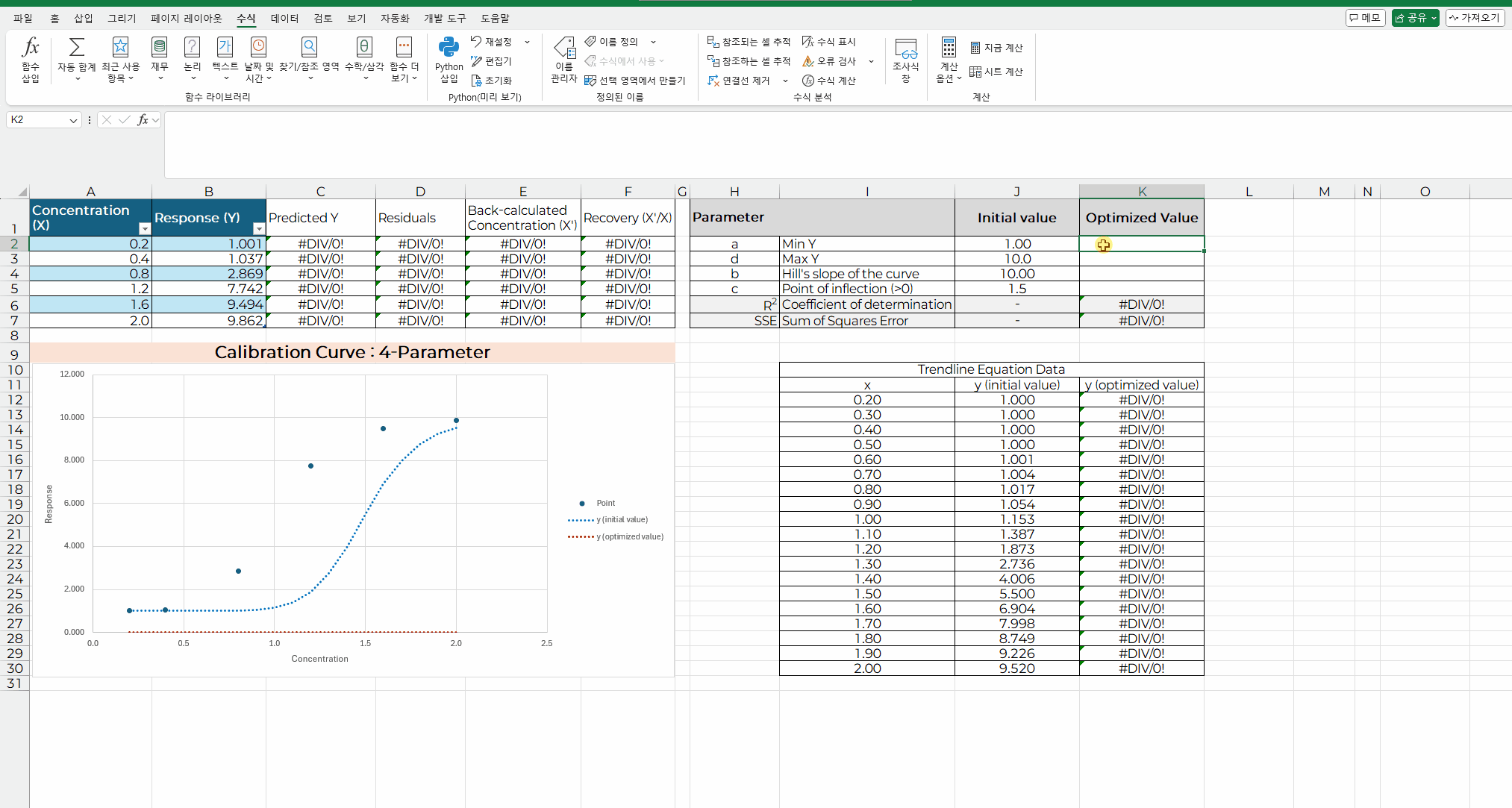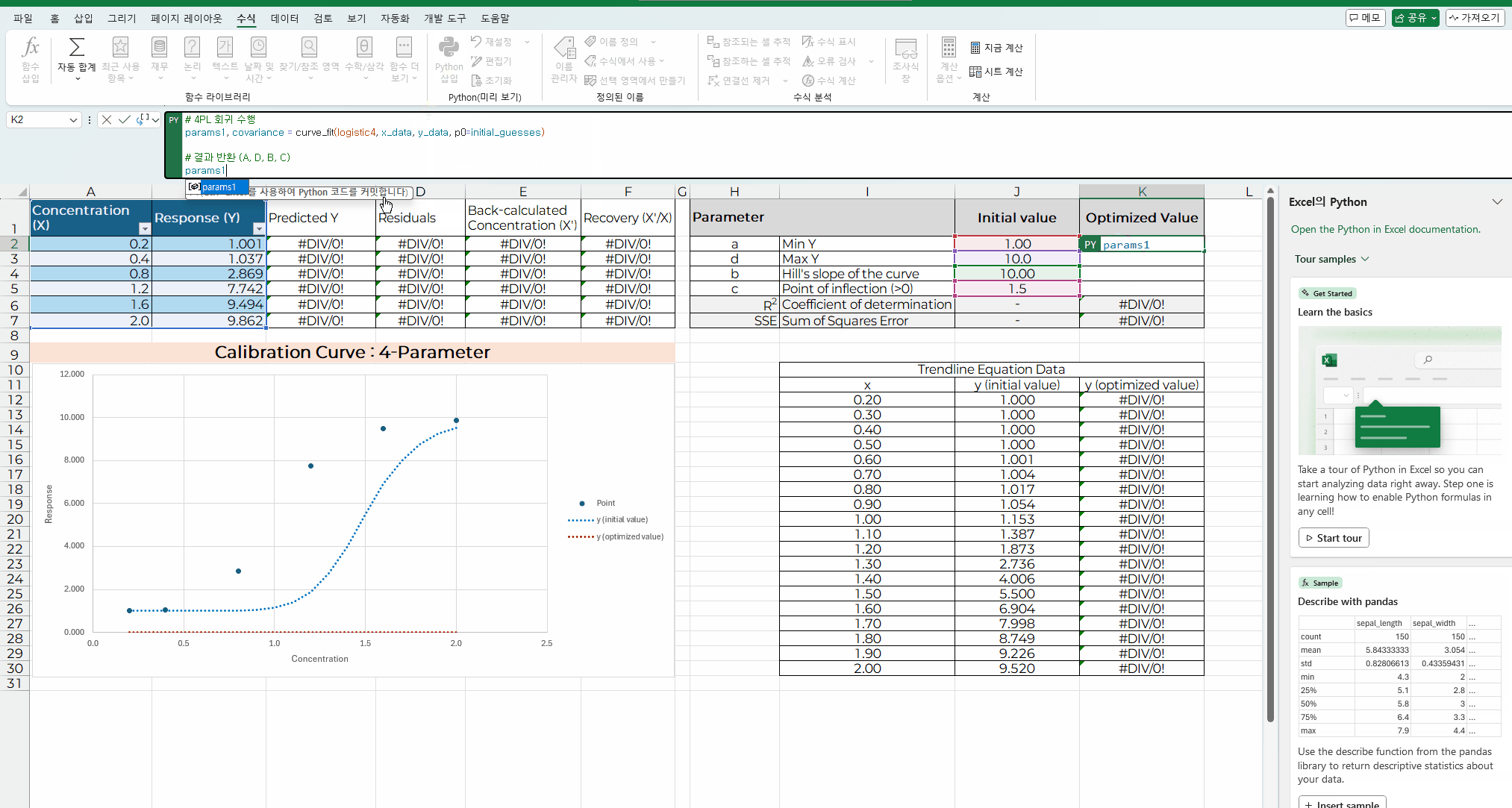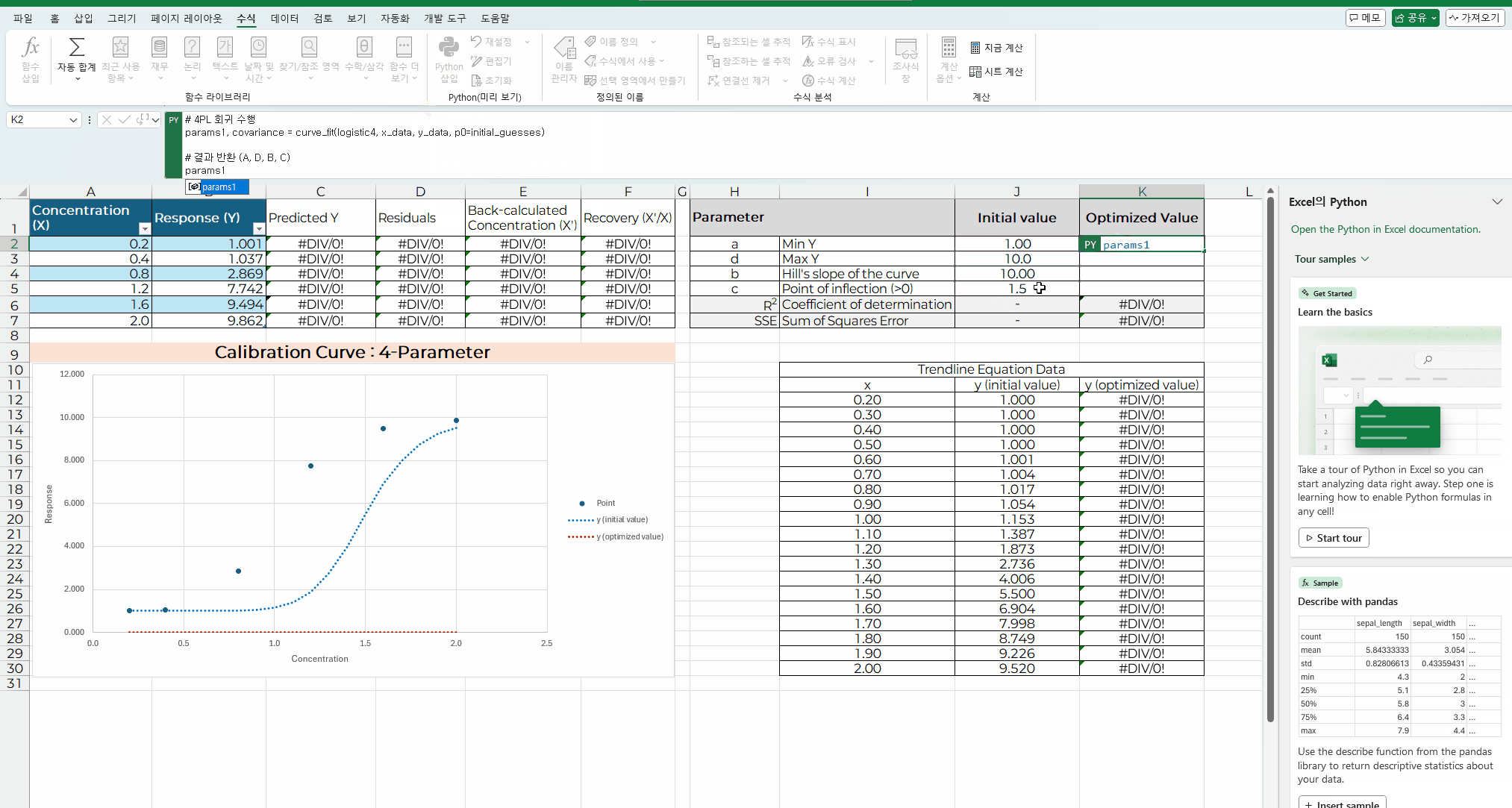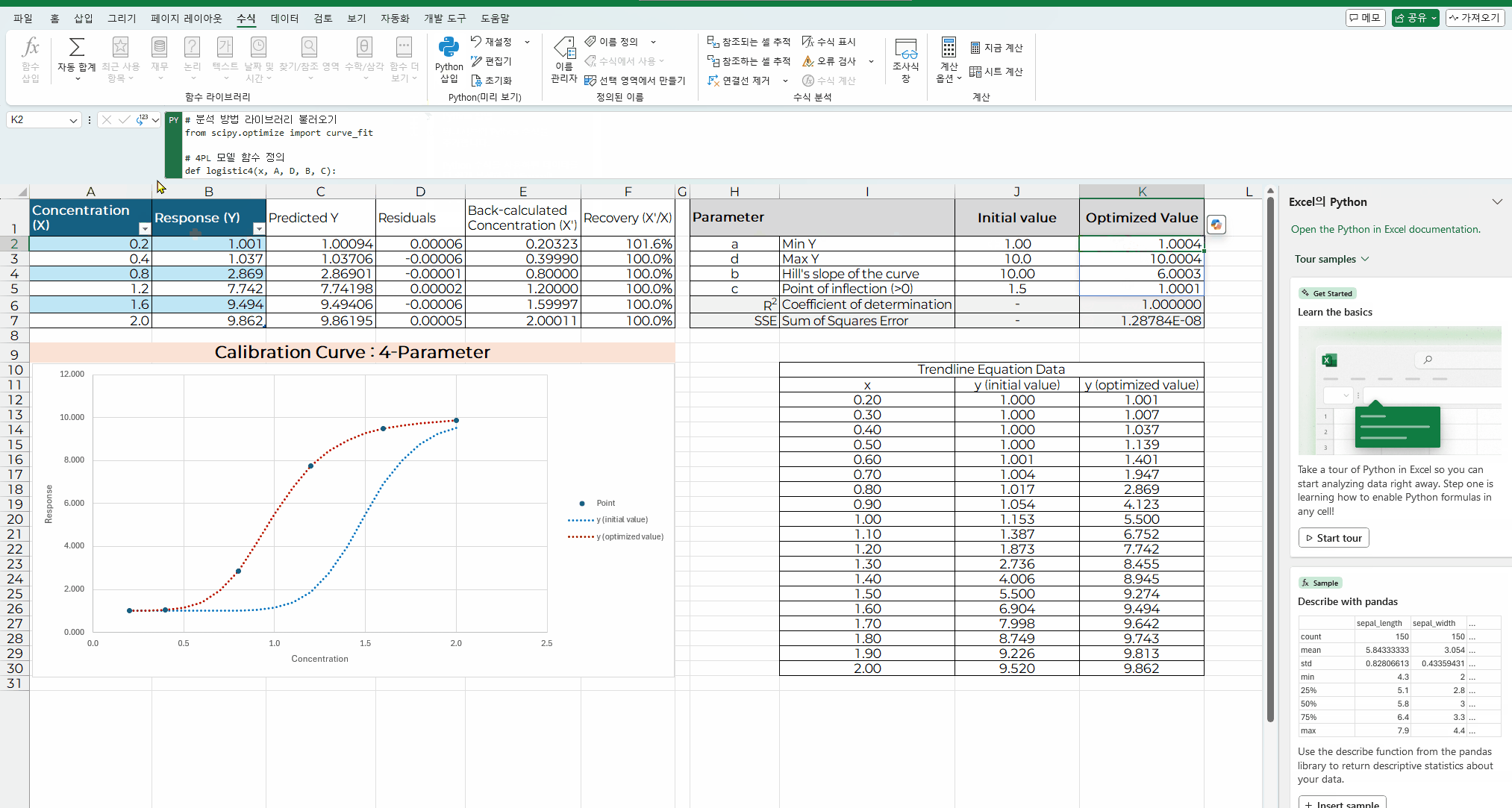
이전 처럼 해 찾기 기능은 초기값이 최적값과 차이가 있으면
여러차례 반복해서 해 찾기를 수행해야만 최적화된 결과를 얻을 수 있었지만
파이썬 함수로 한번에 최적화된 결과를 자동 계산으로 얻을 수 있었다.
코딩 내용을 입력할 셀에 "=py"입력하거나, "Python 삽입"을 메뉴를 선택한다.
해당 셀에 코딩 내용을 입력하고, "Ctrl+Enter" 를 입력하면 계산이 실행된다.
처음 결과 내용은 바로 보이지 않고, "[py] ndarray" 라고 표기되며
코딩 입력 창 옆에 아래 화살표를 클릭해서 메뉴 중 "Excel 값"을 선택하면 상수값이 나타난다.
파이썬 결과 내용이 4개 상수가 계산되어 출력되어 있기 때문에
python 개체 형태는 배열로 된 값을 포함하고 있어서 해당 셀을 클릭해야 결과를 볼 수 있다.
Excel 값으로 선택하면 여러개의 셀에 각각의 값이 배열되어 나타난다.
하지만, 해 찾기에서 나타나던 문제점으로
초기값과 최적값의 큰 차이가 있으면 발생되던 오류는 파이썬에서도 동일하게 나타났다.
위와 같은 문제를 해결하기 위해서
초기값이 적절한지 확인할 수 있도록 실험 데이터에
초기값으로 설정된 그래프가 적절한지 확인하기 위한 내용이 확인할 수 있도록 내용을 추가하였다.
아래 그림 내용은 초기값 그래프와 최적값 그래프를 비교한 결과이다.
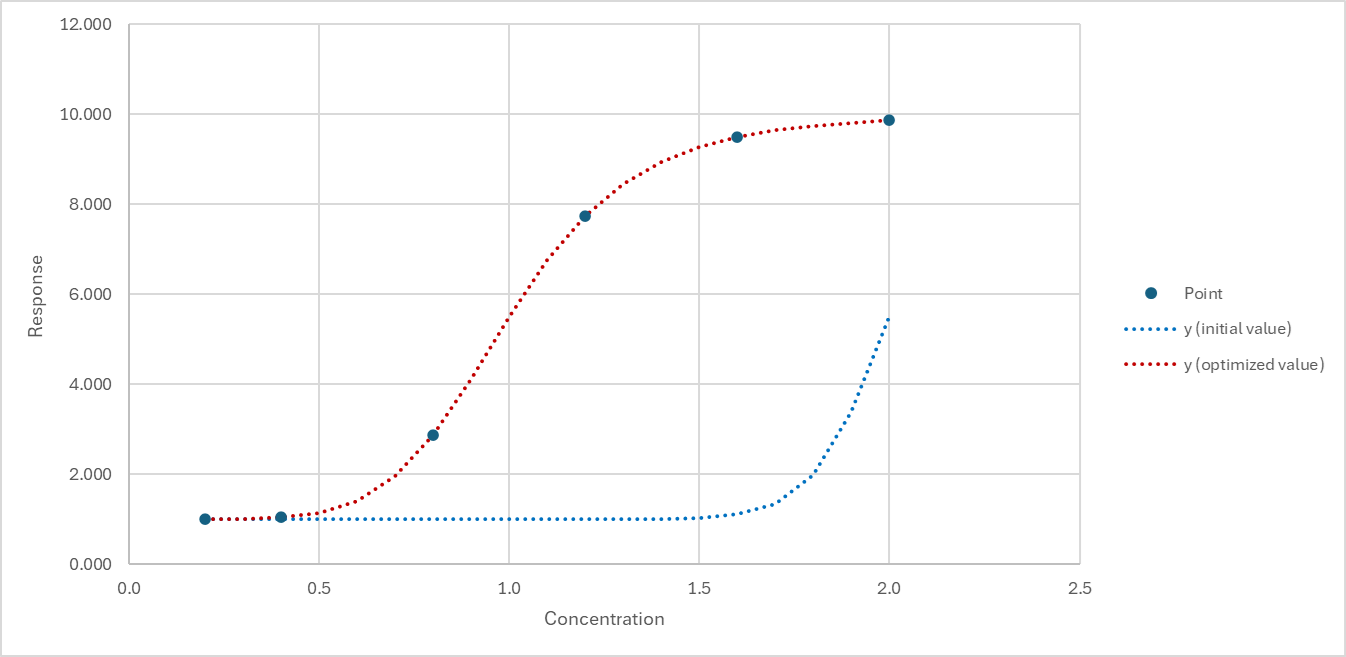
초기값과 최적값의 오차가 어느 정도 있어도 파이썬 방법은 최적화 상수를 한번에 계산하는 것을 확인할 수 있었다.
이전 글에서 엑셀의 해 찾기 기능과 잔차 계산을 사용하면
Levenberg-Marquardt algorithm과 동일한 결과와 얻을 수 있다는 것을 확인했다.
파이썬 방법도 동일한 알고리즘을 사용하기 때문에 해 찾기 결과와 차이가 있는지 확인이 필요했다.
같은 실험 데이터와 동일한 초기값을 설정하고,
각기 다른 방법으로 최적값을 확인했을 때
두 방법 모두 동일한 최적값을 계산되는 것을 확인할 수 있었다.
엑셀 해 찾기 방법은 파이썬 방법과 동일한 결과를 얻을 수 있는 장점이 있지만,
잔차를 추가로 계산해야 최적의 상수값을 얻을 수 있었다.
파이썬 방법으로 4-parameter equation 만드는 방법은 잔차 계산이 없이도 최적의 상수값을 찾는데 어려움이 없었다.
하지만, 파이썬 기능의 사용 여부와 코딩에 이해도가 부족하면 적용하기가 어렵다는 단점이 있었다.
자세한 내용은 첨부된 엑셀 파일로 확인할 수 있습니다.
'기기분석 데이터' 카테고리의 다른 글
| [Excel & Python] 비선형 검정곡선 : Weighted 4-Parameter Equation (0) | 2025.04.10 |
|---|---|
| [Excel] 비선형 검정곡선 만들기 : 4-Parameter Equation (0) | 2025.04.03 |
| [Excel] 회귀분석 (Regression) - 이차방정식 (Quadratic Equation) (0) | 2024.10.21 |
| 검정곡선 (Calibration Curve) 농도 설정과 반복 측정 (2) | 2024.09.23 |
| [Excel] 단순 선형 회귀분석 (Simple Linear Regression) : 검정곡선 (Calibration Curve) 검증 (0) | 2024.08.19 |